每天学习一点：关于噪声（noise）的知识说明

噪声（noise）是一个令人困惑的术语。实际上，不难看出原因。因为理解它意味着量化随机和混乱行为的含义。从根本上说，噪声（noise）腐蚀，掩盖，隐藏它共存的信息。我们如何处理这个问题？好吧，就像我们处理设计电路或芯片的过程一样。该过程首先要了解和理解基本电子元件的行为-如电阻器，电容器，传输线等。

接下来，我们需要一种组合这些个体行为的方法来预测我们正在设计的整个电路或器件的聚合行为。该理论存在并且非常先进，并且存在于我们用于简化电路分析的CAD工具中。因此，我们可以集中精力创造我们想要的表现，而不是被计算过程的细节所困扰。此外，我们可以使用这些工具的基本结果，如电流和电压，将它们转换为一组标准输入-输出性能参数-增益，功率，效率等-并转换为允许一个电路分析结果与另一个独立电路分析的结果相结合的网络参数。碰巧它只需要四个复数的变量（参数）来描述任何给定频率下特定线性网络的所有互连组件的聚合行为，可以使用网络参数，如S参数，Y参数，ABCD参数等来分析它们。

事实证明，我们可以使用仅2个实数变量加1个复数变量（4个值）类似地预测给定频率下噪声电路的总体行为。1956年，在这个方向的第一步是Rothe和Dahlke证明我们可以用一个相同的无噪声电路代替任何线性噪声双端口电路，然后是噪声电压源和噪声电流源的串并联组合。虽然这两个噪声源代表随机过程，但它们之间可能存在某种程度的相关性。所得组合的电路性能与原始电路行为相同。另请注意，标记为‘en’和‘in’的噪声源是统计电压和电流源，其RMS电压和电流与噪声功率成比例。两个噪声源位于无损网络的输入端，称为输入参考噪声源，因为所有内部噪声源已经组合并转换到了输入。

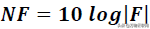
噪声源的等效电路

噪声

与线性电路分析的网络参数（功率，增益等）一样，我们定义噪声网络参数，如噪声系数，噪声因子和噪声温度。这些术语用于量化网络中产生的噪声量。

可用信号功率与不需要的可用噪声功率（SNR）的比率是明显的性能度量，其量化噪声破坏共存的期望信号的程度。电路的噪声因子（F，noisefactor）是另一个度量，可能是描述电路行为的最常用参数。它被定义为电路输入端的信噪比除以输出端的信噪比。只要输入和输出数据的测量带宽相同，噪声系数始终大于1。没有任何噪声源的网络的噪声系数为1。组件的噪声系数测量该组件产生额外噪声的程度，以使其更难以看到所需信号。此讨论的主要目标之一是显示此性能指标的重要性以及如何为给定电路计算它。

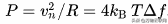
噪声因子的表示式

噪声系数（NF，NoiseFigure）是以dB表示的噪声因子（NoiseFactor）：

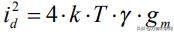
噪声系数

对于无源器件，NF的计算是非常简单的，因为它与以dB为单位的器件损耗相同。噪声系数和噪声因子的定义适用于任何电气网络，包括包含混频器和IF放大器（上变频器或下变频器）的变频网络。

约翰逊噪声（JohnsonNoise）

温度是量化集合行为的一种方式，如气体中粒子的行为。噪声电压是指定或量化随机性的另一种方式，例如电子元件内电荷的随机运动。玻尔兹曼常数（k=1.38065*10^-21焦耳/开尔文）是宏观和微观物理学之间的统计桥梁，有助于我们开始理解和量化噪声。

在1928年最重要的论文之一中，奈奎斯特（Nyquist）利用热力学均分定律表明，在热力学平衡和绝对温度T（开尔文）下由电阻R组成的热力学系统可以表征为RMS高斯噪声电压，其中功率与电压，温度和带宽有关：

噪声功率与RMS噪声电压的之间的关系

这个RMS噪声电压既不取决于材料也不取决于电路的配置，这是一个惊人的事实。相反，控制它的表达式相对简单，仅取决于温度，带宽和玻尔兹曼常数。这也意味着我们可以在用相同值的无噪声电阻器及其相关的串联RMS电压源替换每个噪​​声电阻器后，使用标准电路分析来模拟噪声电路的噪声行为。

最后，注意约翰逊的噪声功率与相关电阻和频率的值无关！

经过一番思考后，这似乎有点傻。躺在桌子上的电阻器正在发电吗？诀窍在于电阻器处于热平衡状态，因此它正在消耗的能量与它接受到的能量一样多。1926年，贝尔实验室的首先发现了这种类型的噪声。他将他的发现描述给贝尔实验室的HarryNyquist，他能够解释结果。使用电流和电导代替电压和电阻，有一个Norton等效RMS电流表达式。

IEEE室温标准为290开尔文。因此，在290Kelvin的“标准温度To”下，1Hz带宽的热噪声功率（kTB）为4.005x10^-21W或-172.75dBm-假设是频率不相关的平坦（白色）噪声功率谱。

另一种观察约翰逊噪声功率方程的方法是注意，对于给定的带宽和噪声功率，我们可以定义一个与噪声功率谱密度（P/B）成正比的独特温度，其中P为噪声功率，B和带宽。我们可以将其称为噪声系数为F的元件的有效噪声温度，这是我们常用的命名法。

Te=290（F-1）

散粒噪声（ShotNoise）

ShotNoise

在大多数电子电路中，散粒噪声和约翰逊噪声是最常见的噪声源。两者都是“白噪声源”，与频率无关，但它们绝不是唯一的噪声源。

晶体管的沟道噪声

FET和其他晶体管具有取决于器件沟道饱和特性的热电流噪声源，并且它类似于约翰逊噪声，使用gm作为跨导，伽马（gamma）作为常数，其值在0.67和1.5之间变化。

TransistorChannelNoise

闪烁噪声（FlickerNoise）

另一种噪声称为闪烁噪声或1/f噪声或粉红噪声。闪烁噪声表现出反频率功率密度曲线，并且通常以由低频闪烁噪声支配的区域和高频“白噪声（whitenoise）”噪声之间的角频率fc（cornerfrequency）为特征。

器件的闪烁噪声功率由RMS电流描述，该电流与流过器件的直流（或平均）电流（i）及其相关角频率成正比：

FlickerNoise

其中Kf是一个常数，取决于材料的类型，1m3，1n3。

量子噪声（QuantumNoise）

存在称为“量子（Quantum）”噪声限制的东西，其确定高增益“线性放大器（linearamplifier）”的噪声温度Tn的最低值。

量子噪声温度

由普朗克常数，玻尔兹曼常数和工作频率定义。这意味着“线性放大器”必须为其处理的任何信号增加噪声功率，无论多小。在10GHz时，就有效噪声温度而言，这相当于约500mKelvins-听起来很难测量。

我们可以用图形方式说明具有热，噪声，闪烁和量子噪声源的典型噪声分量的行为，如下所示。

各种噪声的频率分布

噪声参数

正如电路分析中一样，可以通过一组网络参数（例如S参数，ABCD，Z和Y参数）在每个频率上描述各个电子元件集合的聚合行为，即聚合噪声行为。可以通过称为噪声参数的一组数据来描述一组互连的噪声分量。

有许多等效的最佳噪声参数集，它们都产生相同的结果。最常见的集合包含Fmin，Rn和最佳源匹配（OptimumSourceMatch）（复数），另一个等效集合包含Tmin，N和最佳源匹配（OptimumSourceMatch）（复数）。这些参数允许您预测整个电路的噪声行为，而不必计算所有单独的噪声功率，然后将它们转换为最终的总噪声性能。源匹配是指Gammaopt或Yopt或Zopt。从设计的角度来看，这可以告诉您，如果设计的源阻抗为Zopt，则您的设计会产生最佳噪声系数。此外，它还计算了输入端的任何源阻抗情况下电路的噪声系数。

大多数时候，我们正在设计需要有源器件（例如晶体管）的东西来实现我们的设计目标。噪声参数可帮助您比较晶体管器件选项并决定使用哪个晶体管，然后如何优化晶体管嵌入电路的噪声性能。噪声系数是量化我们网络噪声性能的指标，因此我们需要确定它与噪声参数的关系，以便能够在我们的设计中使用它们。

噪声因子（噪声系数）

我们关心噪声，因为它往往会破坏或掩盖我们希望接收或处理的微弱的有用信号。显然，如果我们希望使用的输入信号的功率电平与混合噪声的功率电平相当，那么我们就会有辨别所需信号的问题。由于电路设计中的每个电气元件都是有损元件或形成频率响应的无损元件，因此电路的输出信噪比降低，而并且基于下面定义的噪声系数将增加：

噪声因子

在噪声因子的定义中，输入噪声功率密度总是kTo，或-172.75dBm/Hz，To等于290K，信噪比（SNR）定义为信号功率（有意义的信息）与背景噪声（无用信号）的功率之间的比值。灵敏度是另一个网络参数。它表示产生具有指定信噪比的指定输出信号或一些其他指定标准所需的最小输入信号功率。

下面的框图允许我们研究噪声因子F：

研究噪声因子F的框图

将这些变量代入噪声因子方程导致下面的方程：

噪声因子方程

噪声系数方程

其中Ni=kToB，定义为Nx，Nx是器件增加的噪声，Nx=kTeffB。

这是一些好消息。您无需计算或测量任何内容即可了解无源线性网络的噪声系数。它只有1/G（插入损耗）。另请注意，增益表达式是“可用功率增益”，而不是常见的传导功率增益（TransducerPowerGain）（S21）。可用增益（AvailableGain）是当共轭输出负载匹配时，网络功率输出与源可用功率之间的比率，可用增益（AvailableGain）始终与特定源阻抗相关。噪声计算使用可用增益（AvailableGain），并且通常通过将输出噪声功率除以可用增益来来将该噪声功率参考为输入。

我们可以重写噪声因子方程，以突出显示与输入相关的可用输出噪声的使用（Nout，i=Nx/G）。结果是噪声系数定义为1加上输入参考噪声功率除以输入噪声功率。

噪声因子的另外一种表示

最佳噪声因子（OptimumNoiseFactor）

我们都希望设计出最好的电路，并在1969年的另一篇关于噪声行为的重要论文中，RLLane推导出一个表达式，它将基本噪声参数Fmin，Rn和YsOpt与给定频率下并为特定的输入导纳Ys的器件的噪声因子联系起来。这为我们提供了一个很好的工具来计算我们需要提供给有源器件的源阻抗，以优化电路噪声系数。

噪声因子的另外一种表达形式

或者，噪声因子可以由噪声温度指定，在某些情况下更方便：

用温度来等效噪声因子

其中Te的常数值或等效的Fmin导致特定网络的输入导纳（Ys）的轨迹，该特定网络在史密斯圆图中形成圆，在圆的中心具有最佳输入导纳Yopt。如果在单个史密斯圆图上组合噪声圆和增益圆，则这些圆的重叠将为您提供同时满足特定的增益和噪声性能的输入导纳范围的可视化图形。该图形快速显示噪声和增益之间的设计权衡。当然，最佳噪声性能源匹配也不太可能是增益的最佳源匹配-尤其是在一系列频率范围内。

评估噪声参数

至少有两种方法可以建立网络或晶体管的噪声参数：

一种是在每个频率进行四次噪声因子测量，其中每次测量使用不同的已知输入源导纳。使用该数据解决每个频率下4个未知噪声参数的Lane公式。

第二种方法是强力方法（bruteforce），用无噪声分量及其各自的噪声电源替换网络的所有噪声分量，然后使用电路分析计算确定计算所需SNR所需的信号和噪声功率给定Ys的噪声系数。如果这是一个代数表达式，则表达式的导数将导致最佳噪声参数。

第三种方法是使用电路分析将各个噪声源引用到输入，注意任何有噪声的线性双端口网络都可以简化为具有单个电流和单个电压噪声源的无噪声网络，尽管这两个源可以相互关联。将噪声源引用到输入所需的电路分析可以经常使用Thevenin和Norton理论来找到等效的输入参考噪声源及其相关性。

噪声分析框图

一旦根据噪声电路计算了in和en源，就知道gn，Rn和ρ。根据这些值，我们可以使用Pospieszalski方程（1）计算噪声参数，以确定最佳噪声因子方程的其它项：

（1）在他的MTT微波杂志上发表的关于“InterpretingTransistorNoise”的文章，IEEEMicrowaveMagazine，vol。11，，，2010年10月.doi：10.1109/

Lane的噪声因子方程的推导细节以及噪声参数与任何线性双端口电路的电路元件和噪声源之间的关系都有所涉及，我将参考Marian的论文中的参考文献。数学细节相对简单，但非常繁琐。

一个简单的例子

好吧，大概就是这样的。我想用一个简单的例子来完成，但你会在数学的破碎乏味中入睡-即使对于只有依赖电流源，栅极电容和电阻以及漏极电阻的简单FET模型。所以，相反，我向你展示了JoeBardin的杰出作品，他模仿了IBMSiGeHBT，并使用上面显示的基本方法，以高精度预测SiGe器件的噪声参数（和S参数）。这是他使用的模型，其目的是将基极电流和集电极电流分解为正向和反向分量。该模型包括噪声电阻RB，RE和RC，以及基极和集电极电流噪声贡献的散粒噪声电流。

晶体管噪声的等效分析电路

在经过大量繁琐的数学计算后，这个模型的分析得出的噪声参数-请查看下面引用的论文的定义和近似值。

噪声分析公式

最后，证明所有这些理论真正适用于真正的硬件。下面是晶体管的噪声系数与频率的关系，显示了测量和计算的性能。

上述分析所得到的噪声系数与频率之间的关系

参考文献：

,,,"Ultra-Low-PowerCryogenicSiGeLow-NoiseAmplifiers:TheoryandDemonstration,"inIEEETransactionsonMicrowaveTheoryandTechniques,,,,:10.1109/

很赞哦!（125）